What babies know about numbers

© 2008 – 2022 Gwen Dewar, all rights reserved

What do babies know about numbers?

Back in the 20th century, people assumed that infants lacked "number sense."

Only today'due south cognitive scientists have overturned the quondam ideas.

Experimental research reveals a fascinating new world of baby cognition, one in which babies can

• recognize the approximate difference betwixt two numbers
• go along precise runway of modest numbers, and
• do simple subtraction and addition bug.

Moreover, when babies perform these feats they activate the same parts of the brain that are associated with mathematical thinking in adults.

Here I review recent discoveries. I begin with what babies know about numbers—large and small—and stop with a give-and-take of infant "arithmetic" and the brain.

What babies know about "numerosity"

Psychologists define "numerosity" as the number of things in a set.

Although we can go a precise measure of numerosity by counting, it's possible to capeesh numerosity in a more estimate style.

For instance, if I ask you to glance in a crowded elevator and estimate how many people are in that location, you can probably brand a pretty skillful guess.

Glance within two elevators, and yous'll too be pretty practiced at guessing which ane has more people in it.

All without counting.

It turns out that developed humans aren't the just creatures who can pull this off. A diversity of non-verbal creatures–including monkeys, rats, fish, and homo infants–can detect the approximate difference in magnitude between two sets (Dehaene 1999; Piffer et al 2012).

Show them 2 displays—1 featuring 8 items and the other only iv items—and they will reply differently depending on what they see.

And the difference is appreciable in the brain.

When 3-month old infants were shown a serial of displays depicting dissimilar quantities of objects, the electrical activity of their brains changed in response (Izard et al 2008).

For case, babies were presented with a continuous stream of images, each depicting four objects. From image to paradigm, the objects were bundled differently. Simply the full number of objects remained the aforementioned (run across the first four slides in the epitome below).

Infants subjected to this programme showed signs of colorlessness. Simply their brain activity (every bit measured by outcome-related potentials, or ERPs) would perk upward if they were next presented with an image showing 8 objects (see the fifth, "test" slide in the paradigm higher up).

What'south more, the part of the encephalon that was activated—the parietoprefrontal network—was the same region that lights up when adults procedure information about numbers (Izard et al 2008).

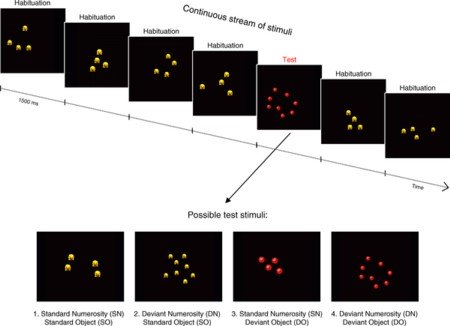
A strong case for "baby number sense"

Were the babies really responding to the change in numerosity? It certainly seems and so.

Babies reacted similarly when presented with pairs of pocket-size numbers (two vs 3) and afar, big numbers (iv vs 12).

And researchers controlled for several, non-numerical variables that could take influenced babies—like the total expanse of the objects, the average area devoted to each object, the full luminance of each image, and the total area occupied past each grouping of objects.

So babies weren't simply attending to the continuous extent of "stuff" in each prototype.

In fact, other experiments suggest that babies pay more than attending to change in number than they practise to changes in continuous extent or surface expanse (Cordes and Brannon 2008).

Nor is it all "in the heart." If babies' feats of numerical discrimination were confined to visible objects, we might suspect that the power is domain specific—a specialization of the visual organization rather than a more full general conceptual ability.

Just babies aren't ane-pull a fast one on ponies. In addition to distinguishing visual arrays, babies can also detect differences in the number of sounds and in the number of deportment (Lipton and Spelke 2003; Wood and Spelke 2005).

Babies can fifty-fifty understand ordinality–the thought that numbers can be arranged in order of magnitude. When xi-calendar month erstwhile babies were presented with sequences of numerosities, they could discriminate betwixt sequences that increased and sequences that decreased (Brannon 2002).

Of form, this doesn't mean that babies can distinguish any two numbers. There are limits. For example:

• Six-calendar month old babies have a hard time distinguishing two quantities if the ratio between them is less than 2:ane. In other words, they tin can handle 8 vs. 16, but fail to distinguish 8 vs. 12 (Xu and Arriaga 2007; Lipton and Spelke 2003).

• Nine- and 10-month olds tin can make effectively distinctions (8 vs. 12). Just even these older babies don't seem to discriminate between eight and ten (Xu and Arriaga 2004; Lipton and Spelke 2003).

• Babies don't distinguish between increasing and decreasing sequences of numbers until the arroyo the end of their first year. When Elizabeth Brannon tested nine-month quondam babies, they failed the test (Brannon 2002).

• Babies' have been stumped by experiments asking them to distinguish a very small number from a larger one (east.g., 2 vs 4 or 2 vs 8). Kristy Van Marle (2013) thinks that'southward because babies rely on unlike mechanisms to make judgments: A precise tracking mechanism for numbers smaller than 4 and an approximate system for judging rough magnitude. Babies don't know still how to integrate the two information sets.

Still, the results are pretty impressive. When babies await at a set of objects, they don't just see a "bunch." Babies have an approximate sense of number.

Do babies act on what they know?

Information technology seems that babies capeesh differences in magnitude. But can babies put this knowledge to any use? Clever experiments advise that they tin can.

In i study, fourteen-month old babies watched experimenters place toys in a box. So experimenters asked the babies "What'southward in the box?" and allow them search.

If a baby had seen only one toy placed in the box, he tended to stop searching after he retrieved that ball. But if he'd seen two balls go in, he'd search longer. Using this method, researchers reported that babies could keep track of upwards to three items (Feigenson and Carey 2003).

In like experiments, 21-month old babies watched while an experimenter placed balls in a box one at a time (Langer et al 2003). Then they were given these instructions:

"One at a time, with one hand, take all the balls out of the box…"

If babies had seen more than than one ball placed in the box, they reached into the box more than once.

Experimenters too ran a trial in which babies saw the experimenter identify two balls in the box, and so pull ane brawl back out. Subsequently watching these trials, babies who were asked to "accept all the balls out of the box" reached into the box only one time.

Baby arithmetic?

These "balls in the box" experiments suggest that babies tin perform other feats–namely, very bones calculations.

Placing two balls in a box–one after the other–amounts to an exercise in addition (1+1). Similarly, removing one of two assurance from a box constitutes subtraction.

So babies who sentry these scenarios—and class the correct inferences—are perchance performing primitive math.

Or are they?

Some researchers accept argued that babies don't solve these issues past doing addition or subtraction. Instead, they are relying on an automated system for tracking objects.

This organisation (which has been studied extensively in adults) appears to runway private objects over fourth dimension by opening a temporary "file" for each one. The brain updates these files every bit objects move or change (Kahneman et al 1992).

The system is limited by memory constraints—the boilerplate person being able to track a maximum of four objects at once. But information technology's an effective organisation for coping with very small numbers.

According to the object file theory, babies discover the sudden absence of an object because there is no longer a match between the set of objects and the set of opened object "files."

Similarly, the brain notices the unexpected appearance of a new object for which in that location is no file.

It's not really arithmetic, then. More than like a perception and memory job.

Simply fifty-fifty if babies use object files, we tin can't dominion out the possibility that babies really exercise understand something nigh addition and subtraction.

To resolve the question, nosotros need to examination babies' noesis of arithmetic without involving their object tracking systems.

And that's exactly what Koleen McCrink and Karen Wynn set out to do.

What babies know about improver and subtraction

Cerebral scientists McCrink and Wynn suspected that babies really could perform numerical computations–if only in a rough, approximate way.

To examination their idea, they presented 9-month former babies with operations involving large number, numbers also large for the object tracking system to handle (McCrink and Wynn 2005).

During the experiment, researchers showed babies several animated films depicting a group of moving rectangles.

In films presenting the addition scenario, 5 rectangles moved around the screen and then hid behind an occluder. Next, 5 more rectangles followed. The movies concluded in one of two ways:

• the occluder moves off to reveal x rectangles (the correct outcome), or
• the occluder moves off to reveal 5 rectangles (the incorrect outcome).

The subtraction scenario was similar, except that it began with 10 rectangles that hid behind an occluder. After, v rectangles slide back "out" and traveled—1 by one—off the screen. The movies ended with either

• the occluder moving off to reveal 5 rectangles (the right outcome), or
• the occluder moving off to reveal ten rectangles (the incorrect consequence).

In both scenarios, babies stared longer at the screen when it displayed the wrong event.

The implications? Babies didn't expect the wrong answers.

They weren't looking longer because they preferred a sure number of rectangles. The incorrect outcomes were associated with different numbers (five for the add-on scenario, 10 for the subtraction scenario).

So it seems that the babies understood two bones points—that addition makes a set more numerous, and subtraction makes information technology less numerous.

Wynn and McCrink concluded that these babies really practice have procedures for numerical calculation, procedures that don't depend on the automatic object-tracking system.

And so how do babies practise it?

It appears that babies–like adults and like many non-human being animals–can track very small sets of objects automatically. They also have the capacity to compare big sets in an imprecise way.

The two feats are distinct and get processed in unlike parts of the encephalon. A study measuring brain activity in 7-calendar month infants reports distinct neural signatures associated with each job (Hyde and Spelke 2011).

And it appears there are specialized neurons for keeping rail of approximate quantities greater than three.

Experiments on monkeys take identified "accumulator neurons," brain cells that are activated by visual displays of objects. The more than objects on display, the more than these special neurons respond (Roitman et al 2007).

The monkey accumulator neurons were found in the aforementioned part of the encephalon that is associated with number-processing in humans. This region–the lateral surface of the parietal cortex–has too been linked with the ability to locate objects in space and fourth dimension.

Then when your infant looks at a large array of objects, it seems likely that specialized accumulator neurons are firing off in her parietal cortex. The neurons respond in a graded fashion, and the extent of their activeness supplies her brain with an guess representation of number.

And the result? A baby that knows the difference between 4 and 8 cookies. Even earlier she knows how to inquire for them by name.

More reading

My article about early on childhood math lessons talks near how to apply opens in a new windowwhat babies know most numbers equally a springboard for introducing toddlers to mathematics.

And for more information well-nigh the minds of babies, check out opens in a new windowthis collection of Parenting Science manufactures.

---

References: What babies know nearly numbers

Brannon EM. 2002. The evolution of ordinal numerical knowledge in infancy. Cognition 83(3):223-40.

Brannon EM, Abbott Southward, and Lutz DJ. 2004. Number bias for the discrimination of large visual sets in infancy. Cognition. 93(two):B59-68.

Cordes S and Brannon EM. 2008. The difficulties of representing continuous extent in infancy: using number is just easier. Child Evolution 79(2):476-89.

Feigensen Fifty, Carey S, and Hauser MD. 2002. The representations underlying infants' choice of more than: object files versus analog magnitudes. Psychological Scientific discipline 13: 150-156.

Hyde DC and Spelke ES. 2011. Neural signatures of number processing in man infants: testify for ii core systems underlying numerical cognition. Dev Sci. fourteen(2):360-71.

Izard V, Dehaene-Lamberz G, and Dehaene S. 2008. Singled-out cerebral pathways for object identity and number in homo infants. PLoS Biol half-dozen(ii):e11.

Kahneman D, Treisman A, and Gibbs. 1992. The reviewing of object files: Object-specific integration of information. Cognitive Psychology 24: 175-219.

Langer J, Gillette P, and Arriaga RI. 2003. Toddlers cognition of adding and subtracting objects in activeness and perception. Cognitive Development 18: 233-246.

Leon MI and Gallistel R. 1998. Self-stimulating rats combine subjective reward magnitude and subjective reward rate multiplicatively. Journal of Experimental Psychology: Animal Behavior Processes 24(3):265-77.

Lipton JS and Spelke ES. 2003. Origins of number sense: Big number discrimination in human infants. Psychological Science 14(5): 396-401.

McCrink K and Wynn Grand. 2004. Large-number addition and subtraction by 9-month-sometime infants. Psychol Sci. fifteen(11):776-81.

Piffer 50, Agrillo C, and Hyde DC. 2012. Small and large number discrimination in guppies. Anim Cogn. 2022 Mar;fifteen(2):215-21.

Roitman, J., Brannon. E.M. & Platt, M.L. (2007). Monotonic Coding of Numerosity in Macaque. PLoS Biology, 5(8).

Vanmarle Yard. 2013. Infants use different mechanisms to make minor and big number ordinal judgments. J Exp Child Psychol. 114(1):102-10.

Xu F and Arriaga RI. 2007. Number bigotry in 10-calendar month-old infants. British Journal of Developmental Psychology 25: 103-108.

Xu F, Spelke ES and Goddard S. 2005. Number sense in human infants. Dev Sci. 8(1):88-101.

content of "What babies know about numbers" last modified 12/12

image of father and child by David R Tribble / wikimedia commons

grimaldiablempoore.blogspot.com

Source: https://parentingscience.com/what-babies-know-about-numbers/

Bagikan Artikel ini